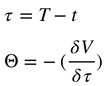
The Greeks

The Black & Scholes (B&S) model allows us to compute the theoretical value of a European option, yet to precisely manage these options, we need a more efficient set of tools : the greeks.

1. Definition

The Greeks are financial indicators allowing us to forecast the way in which an option will move following the modification of different parameters and variables such as :

• The time

• The fluctuations of the underlying asset

• The volatility fluctuation

2. How do we use them ?

Knowing in what measure the value of an option will potentially move, being able to forecast its price fluctuation and hedge against it is crucial for investors regardless of the market and their strategy. On the daily basis the most commonly used greeks on the market are :

• the Delta  ( Δ )

• The Gamma (Γ )

• The Vega ( V )

• The Theta ( θ )

Accordingly we will only focus on those 4 greeks in this article. However, if you want to do financial modeling with some options don’t hesitate to go beyond the scope of this article and learn about the other greeks.

The Delta :

The Delta is defined as the derivative of the option price against the underlying asset.

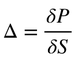
with :

• P = P( t, S, K, r, q, T, θ) : the price of the option
  
• t : the date of valuationS : the price of the underlying
• K : the strike price
• R : the continuous interest rate 

Given the expression of ∆ , for a call option we have :

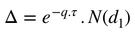
and for the Put option :

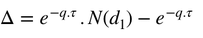
It is also important to keep in mind that :

• ∆ _Call ∈ [ 0;  1]

• ∆ _Put ∈ [ -1 ; 0]
  

The Gamma

The Gamma can be defined as the second derivative of the option price against the underlying. In other words, it is the convexity of the option price against the underlying. 

Call case :

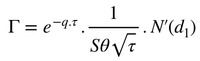
Put case :

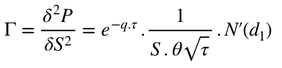
Observation :

• The gamma is increasing as time goes by

• The gamma effect is localised around the strike

• Even near the maturity, an option which is deep in the money or deep out of the money will exhibit a low gamma

Vega ( V ) :

The Vega is defined as the sensibility of the option price to the volatility.

As such for the Call we get :

and for the Put :

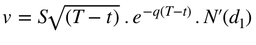
Observation :

• The vega of Call and Put options are identical

• The vega is maximal at the money

• The vega is decreasing as time goes by

Theta (θ ) :

At last, the theta is defined as the opposit of the partial derivative of the option price against the ramining time. In other words, it is the effect of the time on the value of the option.